Equações são expressões algébricas matemáticas que possuem um sinal de igualdade entre duas partes. A intenção de resolver uma equação é determinar o valor da incógnita (valor desconhecido), aplicando técnicas resolutivas. Veja exemplos:
2x + 9 = 5
4x + 10 = 3x – 45
x + 6 = 2x + 12
2*(x + 2) = 3*(x – 3)
Equações exponenciais são aquelas em que a incógnita se encontra no expoente de pelo menos uma potência. A forma de resolução de uma equação exponencial permite que as funções exponenciais sejam também resolvidas de forma prática. Esse tipo de função apresenta características individuais na análise de fenômenos que crescem ou decrescem rapidamente. Elas desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela, como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia entre outras.
Exemplos de equações exponenciais:
10x = 100
2x + 12 = 20
9x = 81
5x+1 = 25
Para resolvermos uma equação exponencial precisamos aplicar técnicas para igualar as bases, assim podemos dizer que os expoentes são iguais. Observe a resolução da equação exponencial a seguir:
3x = 2187 (fatorando o número 2187 temos: 37)
3x = 37 (faz-se o cancelamento das bases)
x = 7 (restando os expoentes)
O valor de x na equação é 7.
Vamos resolver mais algumas equações exponenciais:
2x + 12 = 1024
2x + 12 = 210
x + 12 = 10
x = 10 – 12
x = – 2
2 4x + 1 * 8 –x + 3 = 16 –1
2 4x + 1 * 2 3(–x + 3) = 2 -4
2 4x + 1 * 2 –3x + 9 = 2-4
4x + 1 – 3x + 9 = – 4
4x – 3x = –1 – 4 – 9
x = – 14
5 x + 3 * 5 x + 2 * 5 x = 125
5 x + 3 * 5 x + 2 * 5 x = 5 3
x + 3 + x + 2 + x = 3
3x = 3 – 5
3x = – 2
x = –2/3
2 3x – 2 * 8 x + 1 = 4 x – 1
2 3x – 2 * 2 3(x + 1) = 2 2(x – 1)
3x – 2 + 3(x + 1) = 2(x – 1)
3x – 2 + 3x + 3 = 2x – 2
3x + 3x – 2x = – 2 + 2 – 3
4x = – 3
x = –3/4
2 2x + 1 * 2 x + 4 = 2 x + 2 * 32
2 2x + 1 * 2 x + 4 = 2 x + 2 * 2 5
2x + 1 + x + 4 = x + 2 + 5
2x + x – x = 2 + 5 – 1 – 4
2x = 2
x = 1
Ainda tem duvida? Veja o vídeo.
Agora tente:
a)
b)2x–2 = 16
c)816 + x = 9 –2x
d)2x = 1
e)3x = 27
f)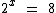
g)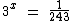
h)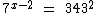
2x + 9 = 5
4x + 10 = 3x – 45
x + 6 = 2x + 12
2*(x + 2) = 3*(x – 3)
Equações exponenciais são aquelas em que a incógnita se encontra no expoente de pelo menos uma potência. A forma de resolução de uma equação exponencial permite que as funções exponenciais sejam também resolvidas de forma prática. Esse tipo de função apresenta características individuais na análise de fenômenos que crescem ou decrescem rapidamente. Elas desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela, como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia entre outras.
Exemplos de equações exponenciais:
10x = 100
2x + 12 = 20
9x = 81
5x+1 = 25
Para resolvermos uma equação exponencial precisamos aplicar técnicas para igualar as bases, assim podemos dizer que os expoentes são iguais. Observe a resolução da equação exponencial a seguir:
3x = 2187 (fatorando o número 2187 temos: 37)
3x = 37 (faz-se o cancelamento das bases)
x = 7 (restando os expoentes)
O valor de x na equação é 7.
Vamos resolver mais algumas equações exponenciais:
2x + 12 = 1024
2x + 12 = 210
x + 12 = 10
x = 10 – 12
x = – 2
2 4x + 1 * 8 –x + 3 = 16 –1
2 4x + 1 * 2 3(–x + 3) = 2 -4
2 4x + 1 * 2 –3x + 9 = 2-4
4x + 1 – 3x + 9 = – 4
4x – 3x = –1 – 4 – 9
x = – 14
5 x + 3 * 5 x + 2 * 5 x = 125
5 x + 3 * 5 x + 2 * 5 x = 5 3
x + 3 + x + 2 + x = 3
3x = 3 – 5
3x = – 2
x = –2/3
2 3x – 2 * 8 x + 1 = 4 x – 1
2 3x – 2 * 2 3(x + 1) = 2 2(x – 1)
3x – 2 + 3(x + 1) = 2(x – 1)
3x – 2 + 3x + 3 = 2x – 2
3x + 3x – 2x = – 2 + 2 – 3
4x = – 3
x = –3/4
2 2x + 1 * 2 x + 4 = 2 x + 2 * 32
2 2x + 1 * 2 x + 4 = 2 x + 2 * 2 5
2x + 1 + x + 4 = x + 2 + 5
2x + x – x = 2 + 5 – 1 – 4
2x = 2
x = 1
Ainda tem duvida? Veja o vídeo.
Agora tente:
a)

b)2x–2 = 16
c)816 + x = 9 –2x
d)2x = 1
e)3x = 27
f)
g)
h)
































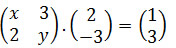
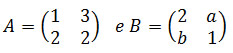
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)