1. A maquete de um edifício foi construída na escala de 1;400.
Se a altura da maquete é de 0,08m. qual é a altura real do edifício?
a.96m
b.48m
c.40m
d.32m
e.24m
2. Marta está jogando bingo com uma cartela de 25 números. Para que ela complete a cartela,estão faltando apenas 5 números.
Se ainda restam 15 números para serem sorteados, qual a probabilidade de sair um número que está faltando para Marta?
a.1/3
b.4/3
c.5/3
d.1/5
e.2/5
3.Uma produtora de vinhos armazena seu produto em recipientes de 54m³.
Quantas garrafas de 750ml podem ser enchidas com o vinho de um desses recipientes?
a.14000
b.40000
c.69000
d.72000
e.80400
4.Uma fábrica de móveis projetou 10 desenhos de mesas escolares e 4 desenhos de cadeiras.
Quantos conjuntos de mesa e cadeira a fábrica pode formar?
a.12
b.24
c.40
d.80
e.210
5.Um poliedro convexo possui 4 faces e 6 arestas.
Qual é o número de vértice desse poliedro?
a.3
b.4
c.8
d.10
e.24
6.Júlia fez compras no valor de 80 reais. como ela pagou à vista, o valor dessas compras caiu para R$72,00.
Qual foi o percentual de desconto obtido por júlia?
a.7,2%
b.8,0%
c.10,0%
d.11,1%
e.15,2%
7.Qual a capacidade total, em litros de uma piscina com 10m de comprimento, 5m de largura e 2,5m de profundidade?
a.12,5
b.125
c.125
d.12500
e.125000
8.Nadia aplicou a quantia de R$1.500,00 durante dois meses, a uma taxa de juros compostos de 2% ao mês.
Quanto Nádia recebeu de juros?
a.R$100,00
b.R$200,00
c.R$202,00
d.R$2.200,00
e.R45.202,00
domingo, 6 de novembro de 2011
quinta-feira, 27 de outubro de 2011
VEM AÍ O SPAECE 2011. ALGUMAS QUESTÕES.
1.O dono de uma fábrica de geladeiras sabe que o número de geladeiras N que ele pode fabricar por mês depende do número x de funcionários trabalhando na fábrica, e essa dependência é dada pela função N(x) = x² + 5x. Qual é o número de funcionários necessários para fabricar 150 geladeiras em um mês?
(A) 5
(B) 10
(C) 15
(D) 20
(E) 25
2.O aluguel de um carro, por dia, é de R$ 20,00 mais R$ 1,50 por quilômetro rodado. Nestas condições, se y representa o valor do aluguel, em reais, e x o número de quilômetros rodados, qual a relação que define essa função?
(A) y = 1,5 + 20x
(B) y = 1,5 – 20x
(C) y = 20 + 1,5x
(D) y = 20 – 1,5x
(E) y = 20x
3.Num quartel, 20% dos militares são oficiais, 70% são soldados. Sabendo-se que há 200 sargentos, qual o número de soldados?
(A) 400
(B) 700
(C) 1000
(D) 1200
(E) 1400
4.Um pintor demorou 2 horas e gastou 1 litro de tinta para pintar uma superfície de 10m2. Nessa mesma proporção, ele projetou os gastos para pintar outras superfícies e organizou como mostra o quadro abaixo.
Área (m2) | Tempo (h) | Tinta (l) |
40 | 8 | 4 |
80 | 16 | 8 |
Para pintar 200m2, ele gastará
(A)8 horas e gastará 4 litros. (B) 24 horas e gastará 12 litros.
(C) 16 horas e gastará 8 litros. (D) 40 horas e gastará 20 litros.
(E) 20 horas e gastará 10 litros.
5.O custo de uma produção, em milhares de reais, de x máquinas iguais é dado pela expressão C(x) = x² – x + 10. Se o custo foi de 52 mil reais, então, o número de máquinas utilizadas na produção foi
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.
(A) 1,0%.
(B) 1,5%
(C) 2,0%.
(D) 2,5%.
(E) 3,0%.
7.A dízima periódica 1,666... é igual a
(A) 85.
(B) 58.
(C) 53.
(D) 35.
(E) 45.
Preciso colocar um piso na área do retângulo, mas a parte do circulo ficará coberta por grama, então a quantidade de m2 de piso necessário para o revestimento do retângulo sem o circulo é:
a) 60m b) 120m c) 314,16m d) 485,84m e ) 800m
1) 9.A Simplificação da expressão –3x – 5y – 3x +6y + 8 - 4x é:
a)19xy b)-4x+y+8 c)-10x+y+8 d) -10x-11y+8 e)-10xy+8
1) 10. João precisa semear uma área de 360m2, observando a recomendação de aplicar 1 kg de milho por 18 m2 de terreno. Quantos quilogramas de milho são necessários para fazer o plantio?
a) 16kg b) 20kg c) 22kg d) 26kg e ) 28kg
segunda-feira, 19 de setembro de 2011
Colégio Estadual Otacílio Mota no ENEM 2010.
Em 2009, o Colégio Estadual Otacílio Mota obteve média 463,84. Entre 929 escolas(No Ceará) com notas divulgadas estava em 555º. Em 2010 nossa média passou para 504,84, houve um avanço, pois, estamos na posição 15968º nacional (Fonte R7.com), quando em 2009 era 17427º e passamos para a posição 451º no Estado.
De forma detalhada é essa nossa situação:
Participantes da prova objetiva: 192. Taxa de participação: 39%. Média em Linguagens e códigos: 443,27. Média em Matemática: 429,09. Média em Ciências Humanas: 474,95. Média em ciências da Natureza: 429,95. Média na Objetivas: 444,31. Participantes da Redação: 176, obtendo média de 570,88. A média total é dada pela média das notas nas objetivas e na redação.
Nota de alunos de escola pública no Enem
De 2009 para 2010, a nota dos alunos de escola pública no Enem (Exame Nacional do Ensino Médio) cresceu 11 pontos, mais do que entre estudantes dos colégios particulares no mesmo período, cujo aumento foi de seis pontos. Com isso, caiu um pouco a distância entre as duas redes de ensino.
De forma detalhada é essa nossa situação:
Participantes da prova objetiva: 192. Taxa de participação: 39%. Média em Linguagens e códigos: 443,27. Média em Matemática: 429,09. Média em Ciências Humanas: 474,95. Média em ciências da Natureza: 429,95. Média na Objetivas: 444,31. Participantes da Redação: 176, obtendo média de 570,88. A média total é dada pela média das notas nas objetivas e na redação.
Nota de alunos de escola pública no Enem
cresce mais que nos colégios particulares
De 2009 para 2010, a nota dos alunos de escola pública no Enem (Exame Nacional do Ensino Médio) cresceu 11 pontos, mais do que entre estudantes dos colégios particulares no mesmo período, cujo aumento foi de seis pontos. Com isso, caiu um pouco a distância entre as duas redes de ensino.
Os números são resultado de mais uma análise das notas do Enem feitas pelo MEC (Ministério da Educação), que até a semana passada tinha divulgado apenas as médias individuais de cada escola.
No ano passado, 221 mil alunos da rede particular fizeram a prova e a média alcançada por eles foi 585,84 pontos – considerando apenas as provas objetivas.
O número de estudantes das escolas públicas que participaram do Enem foi mais do que o triplo (790 mil alunos), e a média foi 16% menor, com 490,28 pontos – uma diferença de 95 pontos no desempenho das duas redes.
Para o MEC, o Enem não é o melhor instrumento para avaliar a qualidade do ensino oferecido pelas escolas, já que a participação dos alunos na prova é voluntária.
Além disso, a prova não mede alguns fatores importantes que têm impacto nesse resultado, como a diferença entre as condições socioeconômicas de alunos de escolas particulares e públicas, a escolaridade dos pais e o investimento feito por aluno, que é bastante superior na rede privada.
A medida mais correta, segundo a pasta, é a comparação do Ideb (Índice de Desenvolvimento da Educação Básica), divulgado no ano passado, que é feito por amostragem. A rede pública alcançou 3,4 pontos no último Ideb contra 5,6 da particular.
O ministério destaca que, comparando os melhores alunos da escola pública com o total de alunos da rede privada, a diferença entre os dois públicos ficou em apenas 7 pontos em 2010, contra 10 pontos em 2009. A média dos 221 mil melhores alunos das escolas públicas foi 578,21 pontos, contra 585,84 do total dos colégios particulares.
Para o ministro da Educação, Fernando Haddad, os números mostram que a “elite” da escola pública tem condições de competir pelas vagas das universidades públicas no mesmo patamar da rede privada.
O ministério destaca que, comparando os melhores alunos da escola pública com o total de alunos da rede privada, a diferença entre os dois públicos ficou em apenas 7 pontos em 2010, contra 10 pontos em 2009. A média dos 221 mil melhores alunos das escolas públicas foi 578,21 pontos, contra 585,84 do total dos colégios particulares.
Para o ministro da Educação, Fernando Haddad, os números mostram que a “elite” da escola pública tem condições de competir pelas vagas das universidades públicas no mesmo patamar da rede privada.
- Isso é importante para sabermos se temos um exército na rede pública em condições competitivas.
Usando as notas obtidas no Enem, o estudante pode pleitear uma vaga em universidades públicas que aderiram ao Sisu (Sistema de Seleção Unificado. Na última edição, foram 83 instituições de ensino participantes.
terça-feira, 30 de agosto de 2011
Calculando raiz quadrada.
Não se sabe ao certo quando nem onde surgiram as raízes quadradas. Admite-se que elas foram muito utilizadas por matemáticos gregos, principalmente após a descoberta do teorema de Pitágoras. O problema começava quando os valores que deveriam ser calculados para as raízes quadradas eram diferentes dos quadrados perfeitos, cuja resposta é exata. Por exemplo, a raiz quadrada de 64 é 8, a de 25 é cinco e assim por diante. Mas, e se necessitarmos calcular a raiz quadrada do número 2? As raízes quadradas são importantes para a resolução de diversos problemas matemáticos, como as equações de segundo grau, e diversos problemas físicos.
Vários métodos foram criados desde aquela época até os dias atuais, todos procurando facilitar cada vez o cálculo destas raízes. Os métodos que ficaram mais conhecidos foram os métodos babilônicos e o das frações continuadas, não só pelos resultados precisos, mas pela rapidez com que eles eram calculados.
Mas existe um método de cálculo de raízes muito simples e também muito preciso. Trata-se do método Marmo para o cálculo de raízes quadradas. Vejamos um exemplo de sua aplicação.
Suponha que você deseja calcular a raiz quadrada de 24. Com uma calculadora isto seria bastante simples. Mas o método Marmo é tão simples quanto. Veja.
Em primeiro lugar, ache a raiz quadrada mais próxima do valor que desejamos (em nosso caso, 24) cujo valor seja exato; neste caso, é a raiz de 25, cujo resultado é 5.
Agora, some os valores que estão dentro das duas raízes:
O resultado será: 49
Pegue o resultado da raiz quadrada cujo resultado é exato, no caso, a raiz quadrada de 25 é igual a 5 e multiplique por 2.
Agora, pegue o resultado da soma das duas raízes, 49, e divida por 10, o resultado da raiz exata multiplicada por 2. Ficará assim: 4,9
Com o auxílio de uma calculadora, vemos que o resultado é 4,89. Portanto, o resultado obtido através do método Marmo é uma boa aproximação do resultado.
Outro exemplo:
- Calcule a raiz quadrada de 35.
Inicialmente, some a raiz de 35 com número mais próximo cuja raiz é exata, neste caso, 36.
Agora, calcule o resultado da raiz quadrada exata e multiplique-o por 2:
Divida o valor encontrado na soma das raízes pelo valor multiplicado por 2 da raiz exata:
Assim, pelo método Marmo para o cálculo de raízes quadradas:
Se compararmos com o valor obtido através da calculadora, 5,9160, vemos que ele também é muito preciso em relação à uma calculadora, por exemplo.
O método Marmo pode ser utilizado para o cálculo de qualquer raiz quadrada e foi desenvolvido pelo Professor Antônio Marmo de Oliveira, um dos maiores especialistas em Matemática Computacional do Brasil.
Prof. Flávio da costa Gonçalves
quarta-feira, 24 de agosto de 2011
TD – FÍSICA 3º ANOS A E B – MANHÃ-2011
COLÉGIO ESTADUAL OTACÍLIO MOTA – TD – FÍSICA 3º ANOS A E B – MANHÃ-2011
PROFESSOR RONALDO PAIVA
Dúvidas no conteúdo? acesse:, http://www.fisicainterativa.com/vestibular/lei_de_ohm/player.html e http://www.fisicainterativa.com/vestibular/corrente_eletrica/player.html
Dica selecione e click com botão direito, escolha ir até o endereço.
1.Dínamos de bicicleta, que são geradores de pequeno porte, e usinas hidrelétricas funcionam com base no processo de indução eletromagnética, descoberto por Faraday. As figuras abaixo representam esquematicamente o funcionamento desses geradores.
Nesses dois tipos de geradores, a produção de corrente elétrica ocorre devido a transformações de energia:
a)mecânica em energia elétrica.
b)potencial gravitacional em energia elétrica.
c)luminosa em energia elétrica.
d)potencial elástica em energia elétrica.
e)eólica em energia elétrica.
2.Uma corrente elétrica de intensidade 16A percorre um condutor metálico. A carga elétrica elementar é e = 1,6 . 10-19 C. O número de elétrons que atravessam uma secção transversal desse condutor em 1,0 min é de:
a) 1,0 . 10^20 b) 3,0 . 10^21 c) 6,0 . 10^21 d) 16 e) 8,0 . 10^19
3. (AFA) Num fio de cobre passa uma corrente contínua de 20A. Isso quer dizer que, em 5,0s, passa por uma secção reta do fio um número de elétrons igual a: (e = 1,6 . 10-19 C)
a) 1,25 . 10^20 b) 3,25 . 10^20 c) 4,25 . 10^20 d) 6,25 . 10^20 e) 7,00 . 10^20
4. (UFMG) Uma lâmpada fluorescente contém em seu interior um gás que se ioniza após a aplicação de alta tensão entre seus terminais. Após a ionização, uma corrente elétrica é estabelecida e os íons negativos deslocam-se com uma taxa de 1,0 x 1018 íons / segundo para o pólo A. Os íons positivos se deslocam-se, com a mesma taxa, para o pólo B. Sabendo-se que a carga de cada íon positivo é de 1,6 x 10-19 C, pode-se dizer que a corrente elétrica na lâmpada será:
a) 0,16A b) 0,32A c) 1,0 x 10^18A d) nula e) n.d.a.
5.(Pucpr) Um estudante de Física mede com um amperímetro a intensidade da corrente elétrica que
passa por um resistor e, usando um voltímetro,mede a tensão elétrica entre as extremidades do resistor, obtendo o gráfico a seguir. Pode-se dizer que a resistência do resistor vale:
a) 0,1 . 10² b) 0,01 .10² c) 1. 10 ² d) 10 ² e) 100 ²
6.
7.
PROFESSOR RONALDO PAIVA
Dúvidas no conteúdo? acesse:, http://www.fisicainterativa.com/vestibular/lei_de_ohm/player.html e http://www.fisicainterativa.com/vestibular/corrente_eletrica/player.html
Dica selecione e click com botão direito, escolha ir até o endereço.
1.Dínamos de bicicleta, que são geradores de pequeno porte, e usinas hidrelétricas funcionam com base no processo de indução eletromagnética, descoberto por Faraday. As figuras abaixo representam esquematicamente o funcionamento desses geradores.
Nesses dois tipos de geradores, a produção de corrente elétrica ocorre devido a transformações de energia:
a)mecânica em energia elétrica.
b)potencial gravitacional em energia elétrica.
c)luminosa em energia elétrica.
d)potencial elástica em energia elétrica.
e)eólica em energia elétrica.
2.Uma corrente elétrica de intensidade 16A percorre um condutor metálico. A carga elétrica elementar é e = 1,6 . 10-19 C. O número de elétrons que atravessam uma secção transversal desse condutor em 1,0 min é de:
a) 1,0 . 10^20 b) 3,0 . 10^21 c) 6,0 . 10^21 d) 16 e) 8,0 . 10^19
3. (AFA) Num fio de cobre passa uma corrente contínua de 20A. Isso quer dizer que, em 5,0s, passa por uma secção reta do fio um número de elétrons igual a: (e = 1,6 . 10-19 C)
a) 1,25 . 10^20 b) 3,25 . 10^20 c) 4,25 . 10^20 d) 6,25 . 10^20 e) 7,00 . 10^20
4. (UFMG) Uma lâmpada fluorescente contém em seu interior um gás que se ioniza após a aplicação de alta tensão entre seus terminais. Após a ionização, uma corrente elétrica é estabelecida e os íons negativos deslocam-se com uma taxa de 1,0 x 1018 íons / segundo para o pólo A. Os íons positivos se deslocam-se, com a mesma taxa, para o pólo B. Sabendo-se que a carga de cada íon positivo é de 1,6 x 10-19 C, pode-se dizer que a corrente elétrica na lâmpada será:
a) 0,16A b) 0,32A c) 1,0 x 10^18A d) nula e) n.d.a.
5.(Pucpr) Um estudante de Física mede com um amperímetro a intensidade da corrente elétrica que
passa por um resistor e, usando um voltímetro,mede a tensão elétrica entre as extremidades do resistor, obtendo o gráfico a seguir. Pode-se dizer que a resistência do resistor vale:
a) 0,1 . 10² b) 0,01 .10² c) 1. 10 ² d) 10 ² e) 100 ²
6.
7.
segunda-feira, 22 de agosto de 2011
Atividade de Matemática 3º anos A e B .23-08-11
Distribuição de frequência em intervalos de classes: Dados contínuos
Para dados quantitativos contínuos, geralmente resultantes de medições de características da qualidade de peças ou produtos, dividimos a faixa de variação dos dados em intervalos de classes. O menor valor da classe é denominado limite inferior (l1) e o maior valor da classe é denominado limite superior (L2).
O intervalo ou classe pode ser representado das seguintes maneiras:
1.onde o limite inferior(l1)da classe é incluído na contagem da frequência absoluta, mas o superior(L2)não;
2.onde o limite superior da classe é incluido na contagem, mas o inferior não.
Podemos escolher qualquer uma destas opções, mas é importante que deixemos claro no texto ou na tabela qual delas está sendo usada. Embora não seja necessário, os intervalos são frequentemente construídos de modo que todos tenham larguras iguais, o que facilita as comparações entre as classes.
Na tabela de distribuição de frequência, acrescentamos uma coluna com os pontos médios de cada intervalo de classe, denotada por xi. Esta é definida como a média dos limites da classe assim, L2 - l1/2(L2 é o limite maior da classe e l1 o menor. ex: 12[-16, onde 12 é l1 e 16 L2) estes valores são utilizados na construção de gráficos.
Algumas indicações na construção de distribuição de frequências são:
Na medida do possível, as classes deverão ter amplitudes iguais.
Escolher os limites dos intervalos entre duas possíveis observações.
O número de intervalos não deve ultrapassar 20.
Escolher limites que facilitem o agrupamento.
Marcar os pontos médios dos intervalos.
Ao construir o histograma, cada retângulo deverá ter área proporcional à frequência relativa (ou à frequência absoluta, o que dá no mesmo) correspondente.
Histograma
Histograma é uma representação gráfica (um gráfico de barras verticais ou barras horizontais) da distribuição de frequências de um conjunto de dados quantitativos contínuos. O histograma pode ser um gráfico por valores absolutos ou frequência relativa ou densidade. No caso de densidade, a frequência relativa do intervalo i, (fri), é representada pela área de um retângulo que é colocado acima do ponto médio da classe i. Consequentemente, a área total do histograma (igual a soma das áreas de todos os retângulos) será igual a 1. Assim, ao construir o histograma, cada retângulo deverá ter área proporcional à frequência relativa (ou à frequência absoluta, o que é indiferente) correspondente. No caso em que os intervalos são de tamanhos (amplitudes) iguais, as alturas dos retângulos serão iguais às frequências relativas (ou iguais às frequências absolutas) dos intervalos correspondentes.
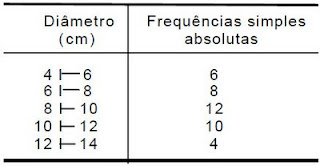
Exemplo de tabela com classes.
Exemplo de Histograma
Num Histograma no eixo x devem ficar os limites das classes e no eixo y as frequências.
Agora é com vocês.
1.Para o Curso de Administração uma classe de uma escola possui as seguintes notas:
36........40........54........31........32........34........43....... 49
50........56........40........42........44........33........54........55
56........59........65........67........50........68........51........54
61........44........39........66........60........36........44........49
36........44........65........42........60........36........54........59
50........69........67........45........69........68........34........55
54........58........32........47........57........25........28........33
a) maior nota;
b) menor nota;
c) amplitude total;
d) tabela contendo: as notas, freqüência relativa, freqüência percentual e Histograma;
e) as cincos melhores notas;
f) as cinco piores notas;
g) classificação das dez primeiras notas;
h) quantas notas estão acima de 75?
i) quantas notas estão abaixo de 45?
j) informe o percentual de notas entre 50 e 68 inclusive.
2.Considere as notas de um teste de inteligência aplicada a 100 alunos:
64....78...66....82.....74....103....78.....86....103....87
73....95...82....89.....73.....92....85.....80.....81....90
78....86...78...101.....85.....98....75.....73.....90....86
86....84...86....76.....76.....83...103.....86.....84....85
76....80...92...102.....73.....87....70.....85.....79....93
82....90...83....81.....85.....72....81.....96.....81....85
68....96...86....70.....72.....74....84.....99.....81....89
71....73...67...105.....74.....98....78.....78.....83....96
95.... 94...88...62.....91.....83....98.....93.....83....76
94.....75...67...95....109.....98....71.....92.....72....73
Faça o rol dos dados , construa uma tabela com frequência relativa e intervalos de classes e faça o histograma.
Para dados quantitativos contínuos, geralmente resultantes de medições de características da qualidade de peças ou produtos, dividimos a faixa de variação dos dados em intervalos de classes. O menor valor da classe é denominado limite inferior (l1) e o maior valor da classe é denominado limite superior (L2).
O intervalo ou classe pode ser representado das seguintes maneiras:
1.onde o limite inferior(l1)da classe é incluído na contagem da frequência absoluta, mas o superior(L2)não;
2.onde o limite superior da classe é incluido na contagem, mas o inferior não.
Podemos escolher qualquer uma destas opções, mas é importante que deixemos claro no texto ou na tabela qual delas está sendo usada. Embora não seja necessário, os intervalos são frequentemente construídos de modo que todos tenham larguras iguais, o que facilita as comparações entre as classes.
Na tabela de distribuição de frequência, acrescentamos uma coluna com os pontos médios de cada intervalo de classe, denotada por xi. Esta é definida como a média dos limites da classe assim, L2 - l1/2(L2 é o limite maior da classe e l1 o menor. ex: 12[-16, onde 12 é l1 e 16 L2) estes valores são utilizados na construção de gráficos.
Algumas indicações na construção de distribuição de frequências são:
Na medida do possível, as classes deverão ter amplitudes iguais.
Escolher os limites dos intervalos entre duas possíveis observações.
O número de intervalos não deve ultrapassar 20.
Escolher limites que facilitem o agrupamento.
Marcar os pontos médios dos intervalos.
Ao construir o histograma, cada retângulo deverá ter área proporcional à frequência relativa (ou à frequência absoluta, o que dá no mesmo) correspondente.
Histograma
Histograma é uma representação gráfica (um gráfico de barras verticais ou barras horizontais) da distribuição de frequências de um conjunto de dados quantitativos contínuos. O histograma pode ser um gráfico por valores absolutos ou frequência relativa ou densidade. No caso de densidade, a frequência relativa do intervalo i, (fri), é representada pela área de um retângulo que é colocado acima do ponto médio da classe i. Consequentemente, a área total do histograma (igual a soma das áreas de todos os retângulos) será igual a 1. Assim, ao construir o histograma, cada retângulo deverá ter área proporcional à frequência relativa (ou à frequência absoluta, o que é indiferente) correspondente. No caso em que os intervalos são de tamanhos (amplitudes) iguais, as alturas dos retângulos serão iguais às frequências relativas (ou iguais às frequências absolutas) dos intervalos correspondentes.
Exemplo de tabela com classes.
Exemplo de Histograma
Num Histograma no eixo x devem ficar os limites das classes e no eixo y as frequências.
Agora é com vocês.
1.Para o Curso de Administração uma classe de uma escola possui as seguintes notas:
36........40........54........31........32........34........43....... 49
50........56........40........42........44........33........54........55
56........59........65........67........50........68........51........54
61........44........39........66........60........36........44........49
36........44........65........42........60........36........54........59
50........69........67........45........69........68........34........55
54........58........32........47........57........25........28........33
a) maior nota;
b) menor nota;
c) amplitude total;
d) tabela contendo: as notas, freqüência relativa, freqüência percentual e Histograma;
e) as cincos melhores notas;
f) as cinco piores notas;
g) classificação das dez primeiras notas;
h) quantas notas estão acima de 75?
i) quantas notas estão abaixo de 45?
j) informe o percentual de notas entre 50 e 68 inclusive.
2.Considere as notas de um teste de inteligência aplicada a 100 alunos:
64....78...66....82.....74....103....78.....86....103....87
73....95...82....89.....73.....92....85.....80.....81....90
78....86...78...101.....85.....98....75.....73.....90....86
86....84...86....76.....76.....83...103.....86.....84....85
76....80...92...102.....73.....87....70.....85.....79....93
82....90...83....81.....85.....72....81.....96.....81....85
68....96...86....70.....72.....74....84.....99.....81....89
71....73...67...105.....74.....98....78.....78.....83....96
95.... 94...88...62.....91.....83....98.....93.....83....76
94.....75...67...95....109.....98....71.....92.....72....73
Faça o rol dos dados , construa uma tabela com frequência relativa e intervalos de classes e faça o histograma.
segunda-feira, 25 de julho de 2011
Constantes fundamentais da natureza estão prestes a mudar.
Constantes fundamentais da natureza
A força eletromagnética ficou um pouco mais forte. A gravidade ficou um pouco mais fraca. E agora se conhece um pouco melhor o tamanho do menor "quantum" de energia.
Os novos valores das constantes fundamentais da natureza, recomendados internacionalmente, acabam de ser divulgados pelo Instituto Nacional de Padrões e Tecnologia (NIST), dos Estados Unidos.
Mas não há motivos para pânico e nem para falsas expectativas: a sua geladeira não passará a grudar no ímã e nem você se sentirá mais leve por uma presumida "dieta da gravidade".
As constantes fundamentais da natureza, que vão de algumas bem famosas, como a velocidade da luz, até outras bem obscuras, como o deslocamento da frequência de Wien, são ajustadas a cada quatro anos, para incorporarem os avanços no conhecimento científico e nas tecnologias e precisões das medições.
Estes últimos valores chegam bem na hora, quando está para ser votado um plano para redefinir as unidades básicas do Sistema Internacional de Unidades (SI), como o quilograma e o ampere, exclusivamente em termos das constantes fundamentais.
Os valores são determinados pela Comissão de Dados para Ciência e Tecnologia (CODATA) - Força Tarefa sobre as Constantes Fundamentais.
Constante alfa
Embora os valores ajustados reflitam alguns desenvolvimentos científicos significativos ao longo dos últimos quatro anos, na maior parte dos casos a melhor notícia que se pode ter sobre o valor de uma constante fundamental é uma redução da incerteza - os cientistas passam a saber o valor com mais precisão.
A incerteza no valor da constante alfa, por exemplo (α = 7,297.352.5698 x 10-3), que determina a intensidade da força eletromagnética, foi reduzida pela metade, chegando agora a 0,3 parte por bilhão (ppb).
Como a constante alfa pode ser medida em uma escala muito grande de fenômenos, a consistência das medições funciona como um barômetro da compreensão geral da física que os cientistas têm.
A constante alfa também será uma constante crítica depois de uma cada vez mais provável redefinição do SI: ela continuará a ser uma constante determinada experimentalmente, enquanto alguns outros valores serão fixados para definir as unidades de medida básicas.
Constante de Planck
A constante de Planck, h, que define o tamanho do menor "quantum" (pacote) de energia possível, e é central para os esforços de redefinição da unidade de massa do SI, também melhorou.
O último valor de h (6,626.069.57 x 10-34 joule/segundo) leva em consideração uma medição do número de átomos em uma esfera de silício altamente enriquecido. Esse valor atualmente não coincide com o outro método fundamental para determinar h, conhecido como o watt-equilíbrio.
Mesmo assim, quando todos os valores são combinados, a incerteza global de h (44 ppb) é menor do que em 2006, e os valores das duas técnicas estão ficando mais próximos um do outro.
Diminuição da gravidade
Os novos valores também incorporam duas novas medições experimentais de G, a constante da gravitação de Newton, que determina a força da gravidade.
O último valor de G (6,673.84 x 10-11 m3 kg-1 s-2) é cerca de 66 partes por milhão menor do que o valor de 2006.
Foram feitos outros ajustes em constantes como o raio do próton e outras constantes relacionadas aos átomos e gases, como as constantes molar e Rydberg.
fonte:http://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=constantes-fundamentais-natureza-mudanca&id=010115110721
A força eletromagnética ficou um pouco mais forte. A gravidade ficou um pouco mais fraca. E agora se conhece um pouco melhor o tamanho do menor "quantum" de energia.
Os novos valores das constantes fundamentais da natureza, recomendados internacionalmente, acabam de ser divulgados pelo Instituto Nacional de Padrões e Tecnologia (NIST), dos Estados Unidos.
Mas não há motivos para pânico e nem para falsas expectativas: a sua geladeira não passará a grudar no ímã e nem você se sentirá mais leve por uma presumida "dieta da gravidade".
As constantes fundamentais da natureza, que vão de algumas bem famosas, como a velocidade da luz, até outras bem obscuras, como o deslocamento da frequência de Wien, são ajustadas a cada quatro anos, para incorporarem os avanços no conhecimento científico e nas tecnologias e precisões das medições.
Estes últimos valores chegam bem na hora, quando está para ser votado um plano para redefinir as unidades básicas do Sistema Internacional de Unidades (SI), como o quilograma e o ampere, exclusivamente em termos das constantes fundamentais.
Os valores são determinados pela Comissão de Dados para Ciência e Tecnologia (CODATA) - Força Tarefa sobre as Constantes Fundamentais.
Constante alfa
Embora os valores ajustados reflitam alguns desenvolvimentos científicos significativos ao longo dos últimos quatro anos, na maior parte dos casos a melhor notícia que se pode ter sobre o valor de uma constante fundamental é uma redução da incerteza - os cientistas passam a saber o valor com mais precisão.
A incerteza no valor da constante alfa, por exemplo (α = 7,297.352.5698 x 10-3), que determina a intensidade da força eletromagnética, foi reduzida pela metade, chegando agora a 0,3 parte por bilhão (ppb).
Como a constante alfa pode ser medida em uma escala muito grande de fenômenos, a consistência das medições funciona como um barômetro da compreensão geral da física que os cientistas têm.
A constante alfa também será uma constante crítica depois de uma cada vez mais provável redefinição do SI: ela continuará a ser uma constante determinada experimentalmente, enquanto alguns outros valores serão fixados para definir as unidades de medida básicas.
Constante de Planck
A constante de Planck, h, que define o tamanho do menor "quantum" (pacote) de energia possível, e é central para os esforços de redefinição da unidade de massa do SI, também melhorou.
O último valor de h (6,626.069.57 x 10-34 joule/segundo) leva em consideração uma medição do número de átomos em uma esfera de silício altamente enriquecido. Esse valor atualmente não coincide com o outro método fundamental para determinar h, conhecido como o watt-equilíbrio.
Mesmo assim, quando todos os valores são combinados, a incerteza global de h (44 ppb) é menor do que em 2006, e os valores das duas técnicas estão ficando mais próximos um do outro.
Diminuição da gravidade
Os novos valores também incorporam duas novas medições experimentais de G, a constante da gravitação de Newton, que determina a força da gravidade.
O último valor de G (6,673.84 x 10-11 m3 kg-1 s-2) é cerca de 66 partes por milhão menor do que o valor de 2006.
Foram feitos outros ajustes em constantes como o raio do próton e outras constantes relacionadas aos átomos e gases, como as constantes molar e Rydberg.
fonte:http://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=constantes-fundamentais-natureza-mudanca&id=010115110721
domingo, 17 de julho de 2011
Email recebido hoje.
Não precisamos de Professores
Não precisamos de EDUCAÇÃO Não precisamos de PROFESSORES
Afinal...
Para que ser um país de 1° MUNDO se está bom assim.
Ronaldinho Gaúcho: R$ 1.400.000,00 por mês.
"Homenageado na Academia Brasileira de Letras"... LETRADO ELE
Tiririca: R$ 36.000,00 por mês, fora os auxílios e mordomias;
"Membro da Comissão de Educação e Cultura do Congresso"...COMO DIZ OS GAUCHOS
- TCHÊ... QUE TAL?
TRADUZINDO, O SALÁRIO DO PALHAÇO AI, PAGA SÓ 30 PROFESSORES, E PARA AQUELES QUE ACHAM QUE EDUCAÇÃO NÃO É IMPORTANTE, CONTRATA O TIRIRICA PARA DAR AULA PARA SEU FILHO.
Um funcionário da Sadia (nada contra) ganha hoje o mesmo salário de um ACT ou um professor iniciante, levando em consideração para trabalhar na empresa você precisa ter o fundamental, ou seja, de que adianta estudar, fazer pós e mestrado?
Piso Nacional dos professores: R$ 1.187,00...
Moral da História:
Os professores ganham pouco, porque só servem para nos ensinar coisas inúteis como:
ler, escrever e pensar.
Sugestão:
Mudar a grade curricular das escolas, que passaria a ter as seguintes matérias:
- Educação Física: Futebol
- Música: Sertaneja, Pagode, Axé
- História: Grandes Personagens da Corrupção Brasileira
Biografia dos Heróis do Big Brother
Evolução do Pensamento das "Celebridades"
- História da Arte: De Carla Perez a Faustão
- Matemática: Multiplicação Fraudulenta do Dinheiro de Campanha
Cálculo Percentual de Comissões e Propinas
- Português e Literatura:
??????????????????????? Para quê??????????? ???????????
- Biologia, Física e Química:
Excluídas por excesso de complexidade
Está bom ou quer MAIS!!!!!!!!!!!!!
ESSE É O NOSSO BRASIL
Passem esta mensagem a TODOOOOOOOOOOOSSSSSSSSSSSSSSSSSSSSS
Atenciosamente :Mauricelio B.da Silva: Ó FÍSICO
quinta-feira, 30 de junho de 2011
quarta-feira, 15 de junho de 2011
VAGAS NO CEARÁ PELO SISU NO IFCE.
As inscrições para o Sisu (Sistema de Seleção Unificada) do MEC (Ministério da Educação) começam às 6h desta quarta-feira (15). Os interessados devem se cadastrar pelo www.sisu.mec.gov.br, até o dia 19 de junho. O sistema funcionará das 6h às 23h59 (horário de Brasília) em todos os dias. As inscrições são gratuitas. Para participar do processo, é obrigatório ter feito as provas do Enem (Exame Nacional do Ensino Médio) de 2010.
São ofertadas 26.336 vagas em 19 universidades federais, 23 institutos federais, dois centros federais de educação tecnológica e quatro universidades estaduais. As vagas estão divididas entre 754 cursos
Instituto Federal de Educação, Ciência e Tecnologia do Ceará
com 1.430 vAGAS
O número de vagas supera em 59% a oferta de vagas do mesmo período do ano passado, que teve a adesão de 35 instituições, com um total de 16 mil vagas.
Resultados
A primeira chamada está prevista para o dia 22 de junho e a matrícula nas instituições de ensino será realizada nos dias 27 e 28 do mesmo mês. A segunda chamada deve acontecer em 2 de julho, com matrícula nos dias 5 e 6 do mesmo mês. O horário e os procedimentos para matrícula deverão ser consultados em cada instituição de ensino.
Entre os dias 2 e 7 de julho, os candidatos que não foram convocados para o curso escolhido como primeira opção poderão manifestar interesse na lista de espera, somente para o curso que foi escolhido como primeira opção. A lista de espera será divulgada em 11 de julho.
Outras informações podem ser obtidas no edital do Sisu ou no site do programa.
São ofertadas 26.336 vagas em 19 universidades federais, 23 institutos federais, dois centros federais de educação tecnológica e quatro universidades estaduais. As vagas estão divididas entre 754 cursos
Instituto Federal de Educação, Ciência e Tecnologia do Ceará
com 1.430 vAGAS
O número de vagas supera em 59% a oferta de vagas do mesmo período do ano passado, que teve a adesão de 35 instituições, com um total de 16 mil vagas.
Resultados
A primeira chamada está prevista para o dia 22 de junho e a matrícula nas instituições de ensino será realizada nos dias 27 e 28 do mesmo mês. A segunda chamada deve acontecer em 2 de julho, com matrícula nos dias 5 e 6 do mesmo mês. O horário e os procedimentos para matrícula deverão ser consultados em cada instituição de ensino.
Entre os dias 2 e 7 de julho, os candidatos que não foram convocados para o curso escolhido como primeira opção poderão manifestar interesse na lista de espera, somente para o curso que foi escolhido como primeira opção. A lista de espera será divulgada em 11 de julho.
Outras informações podem ser obtidas no edital do Sisu ou no site do programa.
Resolução da Prova.
COLÉGIO ESTADUAL OTACÍLIO MOTA – IPUEIRAS – CEARÁ
13ª COORDENADORIA REGIONAL DA EDUCAÇÃO - 13ª CREDE -
UMA ESCOLA DE RESULTADOS – GESTÃO 2009-2012 -
DISCIPLINA:______________MATEMÁTICA____________ SÉRIE:____ TURMA:___ DATA: ___/___/______
PROFESSOR:_____RONALDO PAIVA_____________________________________________________________
ALUNO:______________________________________________________________________
ASSUNTO:___GEOMETRIA ANALÍTICA -CIRCUNFERÊNCIA_________________________________________________________
1. A equação da circunferência que passa pelo ponto (2,0) e que tem centro no ponto (2, 3) é dada por:
a) x² + y² - 4x - 6y + 4 = 0x b) x² + y² - 4x - 9y - 4 = 0
c) x² + y² - 2x - 3y + 4 = 0 d) 3x² + 2y² - 2x - 3y - 4 = 0
e) (x - 2)² + y2 = 9
Resolução:
Primeiro temos que descobrir o raio.
Sendo o raio a distância entre o centro e o ponto da circunferência, temos
dCP=√(2-2)²+(0-3)²=3
(x-2)² + (y-3)²=3² , daí x²+y² -4x-6y+4=0
2. Em qual das alternativas a seguir os dois pontos pertencem à circunferência de equação (x-1)² + (y+5)² = 25?
a)(5,8) e (1,3) b)(-2,-1) e (-3,-4) c)(6,-5) e (1,-1)
d)(4,-9) e (1,0) x e)(0,0) e (3,2)
ampliando a equação, vem:
x² +y²-2x+10y +1=0
verificando por substituição temos que somente d satisfaz.
(4,-9) 16+81-8-90+1=0
(1,0) 1-2+1=0
3. Qual dos pontos a seguir não é interno a x² + y² - 4x -6y = 0?
a) (2,3) b) (3,2) c) (-2,-3)x d) (2,0) e) (0,3)
por substituição tem-se:
(-2,-3) 4+9+8+18, sendo >0, logo, será externo.
4) No plano cartesiano, a circunferência que passa pelo ponto (1,3) e é concêntrico com a circunferência x² + y² -6x -8y -1 = 0 tem a seguinte equação:
a) x² + y² +6x + 8y – 40=0 b) x² + y² -3x -4y +5=0
c) ) x² + y² -6x - 8y +20=0x d) x² + y² +3x + 4y – 25=0
e) x² + y² -3x + 4y – 19=0
raio = √(1-3)²+(3-4)²= √5
(x-3)²+(y-4)² =(√5)² : x²+y²-6x-8y +20=0
5. Para que valores reais de k a equação x² + y² - 2x + 4y –k +3=0 representa uma circunferência:
a)k=2 b)k=-2 c) k>2 d)k<2 e) k>-2x
C(1,-2), a²+b²-r²=0
1²+(-2)²-(-k+3)>0 assim, 5+k-3>0 e k>-2
6) Com relação a reta r 3x -4y +15 =0 e a circunferência λ (x-1)² + (y-2)² = 4, pode-se afirmar que:
a) λ tem centro (-1, 2) e r é externa a λ.
b) λ tem centro (-1,-2) e r é tangente a λ.
c) λ tem centro (1,2) e r é secante a λ.
d) λ tem centro (1,2) e r é tangente a λ.x
e) λ tem centro(-1,-2) e r é secante a λ.
X² +y²-2x-4y+1=0 cujo centro é (1,2)
Isolando a reta vem; x=4y/3 – 5 e substituindo na circunferência:
(4y/3 -5)² + y² - 2(4y/3 – 5) -4y +1 =0
Resolvendo o quadrado perfeito e o produto
16y²/9 -120y +225 +9y² -24y +90 -36y +9=0
Após MMC,
25y² - 180y + 324=0
Fazendo delta ; (-180)² - 4 . 25 . 324, temos 32400 – 32400 =0, logo será tangente.
7. Um sistema de coordenadas cartesianas, em que as abscissas e ordenadas estão em km, foi associado a um mapa mostrando que o epicentro de um terremoto ocorreu no ponto E(3,0). Sabendo que os efeitos desse terremoto foram sentidos, no máximo até um raio de 5km do epicentro. Que equação representaria esse terremoto?
a) x² + y² +3 = 5 b)x² + y² -6x +25=0
c)x² +y² -3x =16 d) x² + y² -6x -16=0x
e) x² + y² -6x + y =25
(x-3)²+(y-0)²= 5², x²+y²-6x-16=0
8) O consumo total de energia nas residências brasileiras envolve diversas fontes, como eletricidade, gás de cozinha, lenha, etc. O gráfico mostra a evolução do consumo de energia elétrica residencial, comparada com o consumo total de energia residencial, de 1970 a 1995.
Fonte: valores calculados através dos dados obtidos de: http://infoener.iee.usp.br/1999.
Verifica-se que a participação percentual da energia elétrica no total de energia gasto nas residências brasileiras cresceu entre 1970 e 1995, passando, aproximadamente, de
a) 10% para 40%. b) 10% para 60%X. c) 20% para 60%
d) 25% para 35%. e) 40% para 80%.
Verifica-se no gráfico, que em 1970 o consumo de energia era de aproximadamente 2,5 . 16^6 tep, em um total de 25 . 10^6tep, o que implica uma participação percentual de 2,5 . 10^6 / 25 . 10 ^6= 0.1 = 10%
Em 1995, o consumo de energia era de 20. 10^6tep em um total de 34 . 10^6, aproximadamente, o que implica 20 .10^6/34. 10~6 = 0, 59 = 60%
terça-feira, 31 de maio de 2011
Teste Vocacional.
Teste Vocacional
A escolha da carreira nunca é facil, sempre surgem dúvidas na hora de decidir entre quais carreiras escolher. O teste vocacional Mundo Vestibular foi elaborado para que você possa descobrir quais carreiras mais combinam com você e com sua personalidade.
Dúvidas, medo e incerteza são questões constantes na vida de todas as pessoas. Em relação a escolha de uma carreira ou profissão não podia ser diferente, algumas pessoas tem uma vocação clara e fica fácil decidir, mas a maioria absoluta se sente perdida quando está prestes a escolher. E neste caso, o que pode ser feito ?
Acesse um dos links e faça o seu teste.
http://www.mundovestibular.com.br/pages/teste_vocacional.html
http://www.oportaldosestudantes.com.br/testevoc.asp
A escolha da carreira nunca é facil, sempre surgem dúvidas na hora de decidir entre quais carreiras escolher. O teste vocacional Mundo Vestibular foi elaborado para que você possa descobrir quais carreiras mais combinam com você e com sua personalidade.
Dúvidas, medo e incerteza são questões constantes na vida de todas as pessoas. Em relação a escolha de uma carreira ou profissão não podia ser diferente, algumas pessoas tem uma vocação clara e fica fácil decidir, mas a maioria absoluta se sente perdida quando está prestes a escolher. E neste caso, o que pode ser feito ?
Acesse um dos links e faça o seu teste.
http://www.mundovestibular.com.br/pages/teste_vocacional.html
http://www.oportaldosestudantes.com.br/testevoc.asp
segunda-feira, 23 de maio de 2011
ENEM 2011.
Iniciam nesta segunda-feira (23) as inscrições para o ENEM 2011 (Exame Nacional do Ensino Médio). Além de o exame ser obrigatório para a adesão do ProUni (Programa Universidade para Todos) e do FIES (Financiamento Estudantil), é pré-requisito mínimo para a participação do SiSU (Sistema de Seleção Unificado), com vagas em diversas instituições públicas de Ensino Superior de todo o país. Interessados têm até as 23h59 do dia 10 de junho para se candidatar exclusivamente pela internet(http://enem.inep.gov.br/).
Nesta edição, a taxa de inscrição custará R$ 35. Segundo especificado no edital, o valor não será devolvido mesmo com a mudança da data da realização do exame. Serão isentos das taxas os estudantes que concluirão o Ensino Médio no ano de 2011 regularmente matriculados em escolas da rede pública, além de candidatos que declarem carência socioeconômica. Os pedidos de isenção devem ser pedidos no ato da inscrição.
As provas estão previstas para serem aplicadas nos dias 22 e 23 de outubro, a partir das 13h, conforme antecipado pelo Universia Brasil. Com a mesma estrutura da edição passada, a avaliação será composta por quatro provas objetivas de múltipla escolha nas áreas de Linguagens e Códigos (Língua Portuguesa, Literatura, Língua estrangeira – inglês ou espanhol -, Artes, Educação Física e Tecnologias da Informação e Comunicação), Ciências da Natureza (Química, Física e Biologia), Matemática e Ciências Humanas (História, Geografia, Filosofia e Sociologia). Cada um dos exames terá 45 questões.
No primeiro dia do exame, serão realizadas as provas de Ciências da Natureza e Ciências Humanas, com duração de 4h30. No domingo, será a vez de Matemática, Linguagens e Códigos e da redação, com tempo de duração mais prolongado (5h30). Os portões de acesso aos locais de prova serão abertos às 12h e fechados às 12h55, de acordo com o horário de Brasília-DF. Não será permitida a entrada de candidatos que se apresentarem após o horário estipulado.
Os gabaritos das provas objetivas serão divulgados até 26 de outubro na página do Inep (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira). A data da liberação do resultado final ainda não foi divulgada.
Leia o edital na íntegra.http://www.in.gov.br/imprensa/visualiza/index.jsp?jornal=3&pagina=40&data=19/05/2011
Nesta edição, a taxa de inscrição custará R$ 35. Segundo especificado no edital, o valor não será devolvido mesmo com a mudança da data da realização do exame. Serão isentos das taxas os estudantes que concluirão o Ensino Médio no ano de 2011 regularmente matriculados em escolas da rede pública, além de candidatos que declarem carência socioeconômica. Os pedidos de isenção devem ser pedidos no ato da inscrição.
As provas estão previstas para serem aplicadas nos dias 22 e 23 de outubro, a partir das 13h, conforme antecipado pelo Universia Brasil. Com a mesma estrutura da edição passada, a avaliação será composta por quatro provas objetivas de múltipla escolha nas áreas de Linguagens e Códigos (Língua Portuguesa, Literatura, Língua estrangeira – inglês ou espanhol -, Artes, Educação Física e Tecnologias da Informação e Comunicação), Ciências da Natureza (Química, Física e Biologia), Matemática e Ciências Humanas (História, Geografia, Filosofia e Sociologia). Cada um dos exames terá 45 questões.
No primeiro dia do exame, serão realizadas as provas de Ciências da Natureza e Ciências Humanas, com duração de 4h30. No domingo, será a vez de Matemática, Linguagens e Códigos e da redação, com tempo de duração mais prolongado (5h30). Os portões de acesso aos locais de prova serão abertos às 12h e fechados às 12h55, de acordo com o horário de Brasília-DF. Não será permitida a entrada de candidatos que se apresentarem após o horário estipulado.
Os gabaritos das provas objetivas serão divulgados até 26 de outubro na página do Inep (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira). A data da liberação do resultado final ainda não foi divulgada.
Leia o edital na íntegra.http://www.in.gov.br/imprensa/visualiza/index.jsp?jornal=3&pagina=40&data=19/05/2011
sexta-feira, 15 de abril de 2011
Exercícios para 3ºs A e B 2011 ( geometria analítica)
1 (FASP) A equação da reta suporte do segmento
AB, dados A(7, 11) e B(15, -1), é:
a) 2y-3y -24=0
b) 3y-2x+17=0
c) 3y-2x+7=0
d) 2y+3x -43=0
e) Nenhuma.
2 (OSEC-SP) A equação da reta que passa pelo
ponto A (3,-4) , e cujo coeficiente angular é
1/2 , é:
a) x+2y+11=0
b) x-y+11=0
c)2x-y+10=0
d)x-2y+11=0
e)nenhuma
3 (PUC-SP) A equação da reta com coefi ciente angular igual a
- 4 /5 ,e que passa pelo P(2,-5), é:
a) 4x+5y+12=0
b) 4x+5y+14=0
c) 4x+5y+17=0
d) 4x+5y+16=0
e) 4x+5y+15=0
4 (PUC-RS) Se as retas 3x-y-7=0, 2x+y+c=0
e 2x-y-5=0 são congruentes, então c é igual a:
a) –3
b) –1
c) 5
d) 7
e) 9
5 (PUC-PR) As retas de equações 3x-4y+1=0
4x+3y-5=0 são:
a) perpendiculares.
b) paralelas.
c) concorrentes.
d) coincidentes.
e) Nenhuma.
6 (PUC-SP) As retas 2x+3y=1 e 6x-ky=1são
pendiculares. Então k vale:
a) 1
b) 2
c) 3
d) 4
e) 6
7 (UFGM) Sejam r e s duas retas perpendiculares
que se interceptam em P(1,2). Se Q(-1,6) pertence
a uma dessas retas, então a equação da outra
reta é:
a) x+2y-5=0
b) x-2y+3=0
c) 2x-y=0
d) 2x+y-4=0
e) 2x+2y+7=0
9-Considere as retas r: y = 2x – 3 e s: 3x – y – 2 = 0. É verdadeira a afirmação:
a) r e s são paralelas b) r é perpendicular a s c) r e s são coincidentesd) r e s se interceptam na origem e) n.d.a
10.(AFA-94) Para que a reta x − 5 y + 20 = 0 seja paralela à reta determinada pelos pontos M(t, s) e N(2, 1), deve-se ter t igual a:
a) 5s/2 - 5 /2
b) -5s + 7
c) -5s +3
d)5s – 3
11. Determinar a equação da reta r que é perpendicular à reta s de equação 3y + 2x – 6 = 0 e
que passa pelo ponto de intersecção entre as retas t: y – 2x + 5 = 0 e u: x = 3.
12.(PUC-RS) A equação da reta que passa pelo ponto P(2,5) e é paralela à reta de equação x – y +2 =0 é:
a)3x – 2y + 4 = 0
b)2x – 3y + 11 = 0
c)x – y + 7 = 0
d) x – y + 3 = 0
e) x – y – 3 = 0
13.Determine K para que as retas 3x + y – 3 = 0 e kx + y + 5 = 0 sejam paralelas.
14. Determine m e k para que as retas mx+y – 3 = 0 e 3x +y +5 = 0 sejam:
a)concorrentes
b)paralelas
c)coincidentes
15.Determinar a equação da reta r, que é paralela à reta s de equação y – 3x + 5 = 0 e que passa pelo ponto P(2, 3).
16.Verificar se as retas abaixo são ou não perpendiculares:
a) r : −2 x + y + 2 = 0 e s : x + 2 y + 2 = 0
b) r : x + 3 y = 0 e s : y = −3x + 11 = 0
17.Determine os valores de m para que as retas r e s sejam retas coincidentes.
r: 3x + 2y + (3m-5) = 0 s: 9x + 6y + (m2-m+2) = 0
18. Determinar a equação da reta r, que é paralela à reta s de equação 2y – 3x + 5 = 0 e que passa pelo ponto P(2, 1).
19. Dê a equação de r. Sabe-se que r // s, s: 2x – y + 5 = 0 e que r passa pela origem.
20. Dê a equação de r. Sabe-se que r passa por T(0, 1) e é perpendicular à s e que s passa por P( 2, 1) e por Q(1, 2).
Entregar dia 25-04-11
sábado, 9 de abril de 2011
Conheça os campos de atuação das Engenharias.

Gosta da área de exatas? Cálculos e ciência são suas paixões? Então com certeza Engenharia seria uma ótima opção para você!
Cada graduação tem características e perfis próprios. Listamos todas as engenharias para você acabar com suas dúvidas e escolher a área que mais lhe interessa. Confira.
Engenharia Aeronáutica
É o ramo da engenharia que se ocupa do projeto e da manutenção de aeronaves e do gerenciamento de atividades aeroespaciais. O engenheiro aeronáutico envolve-se no projeto e na construção de todos os tipos de aeronave, como aviões, helicópteros, foguetes e satélites. [Leia mais]
- Teste profissional: será que Engenharia Aeronáutica tem a ver com você?
- Orientação vocacional: não sou bom em matemática. Posso prestar Engenharia Aeronáutica?
Engenharia Ambiental
É a engenharia voltada para o desenvolvimento econômico sustentável, ou seja, que respeite os limites dos recursos naturais. O engenheiro que atua nessa área desenvolve e aplica tecnologias para proteger o ambiente dos danos causa dos pelas atividades humanas. [Leia mais]
- Teste profissional: Engenharia Ambiental combina com você? Confira!
- Orientação vocacional: qual a diferença entre Engenharia Ambiental e Ciência Ambiental?
Engenharia Cartográfica
É o ramo da engenharia que capta e analisa dados geográficos para a elaboração de mapas. O engenheiro cartógrafo faz pesquisas de campo e cálculos para elaborar mapas e cartas impressas ou digitais. [Leia mais]
Engenharia da Computação
É o conjunto de conhecimentos usados no desenvolvimento de computadores e seus periféricos. O engenheiro da computação projeta e constrói computadores, periféricos e sistemas que integram hardware e software. [Leia mais]
- Orientação profissional: tenho dúvidas sobre o conteúdo dos diferentes cursos de computação.
Engenharia de Alimentos
São as técnicas e os conhecimentos usados na fabricação, na conservação, no armazenamento e no transporte de alimentos industrializados. Esse profissional cuida de todas as etapas de preparo e conservação de alimentos de origem animal e vegetal. [Leia mais]
- Teste profissional: Engenharia de Alimentos combina com você? Confira!
- Vídeo: Veja como é a rotina de um engenheiro de alimentos no Na Real
- Orientação profissional: Engenharia de Alimentos oferece carreira promissora?
Engenharia de Controle e Automação
É o ramo da engenharia que desenvolve e executa projetos de automação industrial. O engenheiro de controle e automação projeta e opera equipamentos utilizados nos processos automatizados de indústrias em geral, além de fazer sua manutenção. [Leia mais]
Engenharia de Horticultura
São os conhecimentos usados no cultivo de plantas medicinais e ornamentais, na silvicultura e na produção de hortifrutigranjeiros. Esse profissional aplica tecnologia de ponta no cultivo de frutas, verduras, legumes, plantas ornamentais, medicinais e aromáticas ou que servem como condimentos. [Leia mais]
Engenharia de Minas
É a engenharia que se ocupa da pesquisa, da prospecção, da extração e do aproveitamento de recursos minerais. O engenheiro de minas localiza jazidas e analisa o tamanho das reservas e a qualidade do minério no local. [Leia mais]
Engenharia de Petróleo e Gás
É o conjunto de técnicas usadas para a descoberta de jazidas e para a exploração, produção e comercialização de petróleo e gás natural. O engenheiro de petróleo e gás atua em petroleiros, refinarias, plataformas marítimas e em petroquímicas. [Leia mais]
- Teste profissional: Será que Engenharia de Petróleo e Gás é a melhor opção?
- Orientação profissional: O curso Engenharia de Petróleo já foi reconhecido pelo MEC?
Engenharia de Segurança do Trabalho
É o ramo da engenharia responsável por prevenir riscos à saúde e à vida do trabalhador. O engenheiro de segurança do trabalho tem a função de assegurar que o trabalhador não corra riscos de acidente sem sua atividade profissional, sejam eles danos físicos ou psicológicos. [Leia mais]
Engenharia Elétrica
O engenheiro eletricista está presente em todos os aspectos que envolvem a energia, desde a geração, a transmissão, o transporte e a distribuição até o uso nas residências e no comércio. Além disso, planeja, supervisiona e executa projetos nas áreas de eletrotécnica, relacionadas à potência da energia. [Leia mais]
- Teste profissional: Engenharia Elétrica combina com você? Confira!
- Vídeo: veja como é o dia a dia de um engenheiro eletricista no Na Real
- Orientação profissional: O que posso estudar antes de entrar em Engenharia Elétrica?
Engenharia Florestal
É o ramo da engenharia voltado para o estudo e o uso sustentável de recursos florestais. O engenheiro florestal avalia o potencial de ecossistemas florestais e planeja seu aproveitamento de modo a preservar a flora e a fauna locais. [Leia mais]
- Teste profissional: Engenharia Florestal combina com você? Confira!
- Vídeo: conheça o cotidiano do engenheiro florestal no Na Real
Engenharia Industrial
É a área que cuida dos recursos necessários à produção industrial. Esse profissional é o típico engenheiro de chão de fábrica, que acompanha de perto a implantação e a manutenção da infra-estrutura industrial, como redes de água e de gás, pontes e esteiras rolantes. [Leia mais]
- Orientação profissional: Engenharia Industrial Mecânica, difere de um curso normal de Mecânica?
Engenharia Mecatrônica
É o ramo da engenharia que desenvolve e executa projetos de automação industrial. O engenheiro mecatrônico projeta e opera equipamentos utilizados nos processos automatizados de indústrias em geral, além de fazer sua manutenção. [Leia mais]
-Teste profissional: Engenharia Mecatrônica combina com você? Confira
Engenharia Naval
É a área da engenharia que cuida do projeto, da construção e da manutenção de embarcações e seus equipamentos. O engenheiro naval projeta a estrutura, os motores e os demais componentes de navios. [Leia mais]
- Teste profissional: está por dentro de Engenharia Naval? É a profissão certa para você? Confira!
Engenharia Sanitária
É o ramo da engenharia voltado para o projeto,a construção, a ampliação e a operação de sistemas de água e esgoto. Esse profissional é fundamental para a preservação da natureza e de seus recursos. [Leia mais]
Engenharia em Tecnologia Têxtil e da Indumentária
São os conhecimentos utilizados na cadeia produtiva têxtil, desde a fabricação de fios até a comercialização do produto final. O bacharel em Tecnologia Têxtil e da Indumentária concebe e desenvolve projetos e pesquisas tecnológicas ligadas à produção têxtil. [Leia mais]
Engenharia Acústica
É o conjunto de conhecimentos usado para desenvolver novos sistemas eletro acústicos e para determinar a intensidade de ruídos e vibrações. O engenheiro acústico desenvolve técnicas e equipamentos para controlar o ruído ambiental visando ao bem-estar das pessoas. [Leia mais]
Engenharia Agrícola
São as técnicas e os conhecimentos empregados no gerenciamento de processos agropecuários. O engenheiro agrícola projeta, implanta e administra técnicas e equipamentos necessários à produção agrícola. [Leia mais]
- Teste: está por dentro de Engenharia Agrícola? Será que ela combina com você? Confira!
- Orientação profissional: Engenharia Agronômica, Agrícola ou de Agronegócios?
Engenharia Biomédica
É a área da engenharia que cuida da concepção de equipamentos médicos, biomédicos e odontológicos, voltados para diagnóstico ou tratamento terapêutico. O engenheiro biomédico projeta a estrutura, desenvolve e monta os equipamentos e faz a sua manutenção corretiva e preventiva. [Leia mais]
Engenharia Civil
Além de projetar, gerenciar e executar obras como casas, edifícios, pontes, viadutos, estradas,barragens, canais e portos, o engenheiro civil tem como atribuição a análise das características do solo, o estudo da insolação e da ventilação do local e a definição dos tipos de fundação. [Leia mais]
-Teste profissional:Engenharia Civil combina com você? Confira!
- Teste: você está pronto para entrar no mercado de trabalho de Engenharia Civil?
- Vídeo na Real: o dia a dia de um engenheiro civil
- Vida de estagiário em Engenharia Civil
Engenharia em Agrimensura
É o ramo da engenharia responsável pelo levantamento e pela medição de terrenos. O engenheiro agrimensor prepara áreas para obras urbanas, de infra-estrutura hidráulica, sanitária, elétrica ou de transportes. [Leia mais]
Engenharia de Aquicultura
É o conjunto de técnicas e conhecimentos usados na criação de organismos aquáticos em cativeiro. O engenheiro de aquicultura projeta, executa e supervisiona a criação de peixes, crustáceos, moluscos e plantas aquáticas. [Leia mais]
Engenharia de Energia
É o ramo da engenharia que planeja, analisa e desenvolve sistemas de geração, transporte, transmissão, distribuição e utilização de energia. [Leia mais]
Engenharia de Materiais
É o ramo da engenharia voltado para a pesquisa de materiais e de novos usos industriais para os materiais já existentes. Esse engenheiro pesquisa e cria materiais, como resinas, plásticos, cerâmicas e ligas metálicas. [Leia mais]
- Teste profissional: Engenharia de Materiais combina com você? Confira!
- Orientação profissional: Como está o mercado para Engenharia de Materiais?
Engenharia de Pesca
É o setor da engenharia voltado para o cultivo, a captura e a industrialização de peixes e frutos do mar. O engenheiro de pesca estuda e aplica métodos e tecnologias para localizar, capturar, beneficiar e conservar peixes, crustáceo se frutos do mar. [Leia mais]
Engenharia de Produção
É o ramo da engenharia que gerencia os recursos humanos, financeiros e materiais para aumentar a produtividade de uma empresa. O engenheiro de produção é peça fundamental em indústrias e empresas de quase todos os setores. [Leia mais]
- Teste profissional: Engenharia de Produção combina com você? Confira!
- Vídeo: Veja como é a rotina de um engenheiro de produção no Na Real
- Orientação profissional: Engenharia de Produção tem muitos cálculos? Como está o reconhecimento no mercado de trabalho?
Engenharia de Telecomunicações
É o segmento da engenharia que se ocupa do projeto, da operação e da manutenção de equipamentos e sistemas de telecomunicações. Esse engenheiro desenvolve e implanta redes de telecomunicações. [Leia mais]
Vídeo: Veja como é a rotina de um engenheiro de telecomunicações no Na Real
Engenharia Física
É a aplicação de conhecimentos da Física na pesquisa e no desenvolvimento de materiais e tecnologias. É uma profissão muito nova no Brasil. A primeira turma formou-se em 2004. [Leia mais]
Engenharia Hídrica
É o setor da engenharia que cuida da exploração, do uso e da gestão da água. Planejar e orientar a utilização das águas de bacias hidrográficas, prevenindo os impactos negativos que elas possam sofrer em consequência de atividades industriais, agrícolas e urbanas, é a principal função do engenheiro hídrico. [Leia mais]
Engenharia Mecânica
É a área da engenharia que cuida do desenvolvimento, do projeto, da construção e da manutenção de máquinas e equipamentos. O engenheiro mecânico desenvolve e projeta máquinas, equipamentos, veículos, sistemas de aquecimento e de refrigeração e ferramentas específicas da indústria mecânica. [Leia mais]
- Teste profissional:Engenharia Mecânica combina com você? Confira!
- Vídeo: Saiba como é a rotina de um engenheiro mecânico no Na Real
- Vídeo: Jazon Barros fala de seu dia a dia como trainee na Mercedes-Benz
- Orientação profissional: Engenharia Industrial Mecânica, difere de um curso normal de Mecânica?
Engenharia Metalúrgica
É o conjunto de conhecimentos empregados na transformação de minérios em metais e ligas metálicas e em suas aplicações industriais. Com profundo conhecimento dos metais e de suas propriedades, esse engenheiro é responsável pelo beneficiamento de minérios e por sua transformação em metais e ligas metálicas. [Leia mais]
Engenharia Química
É a área da engenharia voltada para o desenvolvimento de processos industriais que empregam transformações físico-químicas. O engenheiro químico cria técnicas de extração de matérias-primas, bem como de sua utilização ou transformação em produtos químicos e petroquímicos, como tintas, plásticos, têxteis, papel e celulose. [Leia mais]
- Teste profissional: Engenharia Química combina com você? Confira!
- Vídeo: conheça a rotina de um engenheiro químico no Na Real
- Orientação profissional: "Engenharia Química é um curso muito difícil?"
Engenharia Têxtil
São as técnicas e os conhecimentos utilizados na fabricação e no tratamento de fibras, fios e tecidos e na confecção de roupas. O engenheiro têxtil projeta as instalações, os equipamentos e as linhas de produção de tecelagens e indústrias de confecção de roupas. [Leia mais]
- Teste: Você está por dentro do mercado de Engenharia Têxtil? Será que a profissão é a sua cara?
Fonte: Guia do Estudante
quarta-feira, 16 de fevereiro de 2011
Resolução dos exercícios sobre Prismas.(3º Ano)
Prismas
Um prisma é um poliedro limitado por dois polígonos e paralelos (as bases) e vários paralelogramos (as faces laterais).
A altura do prisma é a distância entre as bases.
Se todas as faces laterais são retângulos, elas serão perpendiculares às bases e então o prisma chama-se prisma reto.
Se as faces laterais não são perpendiculares às bases, chama-se prisma oblíquo.
Um prisma é regular quando tem um prisma reto que cujas bases são polígonos regulares.
As arestas laterais de um prisma são segmentos iguais e paralelos entre si. Nos prismas retos são prependiculares às bases.
Classificação dos prismas segundo o polígono das bases
Conforme os polígonos das bases são triângulos, quadriláteros, pentágonos, etc, o prisma chama-se triangular, quadrangular, pentagonal, etc.
Os prismas rectos cujas bases são polígonos regulares chamam-se prismas regulares.
Quer em objetos de uso corrente, quer na Natureza, encontramos com frequência formas prismáticas.

Área do prisma
Área lateral = Perímetro da base x altura
Área total = Área lateral +2 x Área da base
Volume do prisma
O volume de um prisma reto ou oblíquo, é:
Volume do prisma = Área da base x altura
Recordamos que a altura de um prisma é a distância entre as duas bases. Se o prisma é reto, a altura coincide com o comprimento das arestas laterais.
TD
1) Calcule o volume de um cubo que tem 10cm de aresta.
Solução. O cubo possui todas as dimensões com mesma medida. Seu volume é calculado pela fórmula: V = a3 . Logo V = (10)3 = 1000cm3.
2) Um prisma pentagonal regular tem 20cm de altura. A aresta da base mede 4cm. Determine sua área lateral.
Solução. A área lateral é a soma das cinco áreas dos retângulos que são as faces laterais. Como a base é regular, todas as arestas possuem a mesma medida. Logo, temos:
i) Área de uma face: 4 x 20 = 80cm2
ii) Área lateral: 5 x (80cm2) = 400cm2.
3) Um prisma quadrangular regular tem sua aresta da base medindo 6m. Sabendo que a área lateral do prisma mede 216m², calcule sua altura.
Solução. Se o prisma é regular então suas bases são quadradas. A área lateral é a soma das áreas das quatro faces. Temos:
216 = 4x6xh
h =216/24 h = 9
4) Um prisma reto tem por base um triângulo isósceles de 8cm de base por 3cm de altura. Sabendo que a altura do prisma é igual a 1/3 do perímetro da base, calcule sua superfície total.
Solução. No triângulo isósceles a altura também é mediana.
i) Pela relação de Pitágoras temos:

logo a = 5cm
ii) O perímetro da base vale: 5cm + 5cm + 8cm = 18cm
iii) A altura do prisma vale
1/3 x 18 = 6cm
iv) área total
Ab = 8 x 3 /2 = 12cm²
Al = (8x6)+2 x (5x6) = 108cm²
At= 2x 12 + 108= 132cm²
5) Calcule a área total de um prisma reto, de 10 cm de altura, cuja base é um hexágono regular de 6cm de lado.
Solução. A área total de um hexágono regular vale o sêxtuplo da área do triângulo eqüilátero.
Temos: .

Ab =6x (6²x ṛaiz quadrada de3)/4 = 93,5
Al = 6x6x10 = 360
At = 2 x93,5 +360 = 547cm²
6)Um armário, com a forma de um paralelepípedo de dimensões 0,5m, 2,5m e 4m, deve ser pintado. O rendimento da tinta empregada é de 5m² por litro. Determine a quantidade de tinta necessária para pintar toda a parte interna do armário.
Solução. Calculando a área total, temos: .
At = 2x{(0,5)(2,5)+(0,5)(4)+(2,5)(4)} = 26,5m²
Logo, empregando 5m2 por litro, serão gastos 26,5/5= 5,3 litros.
7)A garagem subterrânea de um edifício tem 18 boxes retangulares, cada um com 3,5m de largura e 5m de comprimento. O piso da garagem é de concreto e tem 20cm de espessura. Calcule o volume de concreto utilizado para o piso da garagem.
Solução. O piso terá a forma de um paralelepípedo muito fino, já que sua espessura é de 0,20m. Esse piso entrará em cada box. O volume de cada piso é V = (3,5) x (5) x (0,20) = 3,5m3. O volume total utilizado nos 18 boxes será V = (18) x (3,5) = 63m3.
8) Dispondo-se de uma folha de cartolina, de 70cm de comprimento por 50cm de largura, pode – se construir uma caixa, sem tampa, cortando-se um quadrado de 8cm de lado em cada lado. Determine o volume desta caixa.

Solução. O desenho mostra a parte retirada de cada lado e a caixa construída na forma de um paralelepípedo.
O volume será V = (54) x (34) x (8) = 14688cm3.
Um prisma é um poliedro limitado por dois polígonos e paralelos (as bases) e vários paralelogramos (as faces laterais).
A altura do prisma é a distância entre as bases.
Se todas as faces laterais são retângulos, elas serão perpendiculares às bases e então o prisma chama-se prisma reto.
Se as faces laterais não são perpendiculares às bases, chama-se prisma oblíquo.
Um prisma é regular quando tem um prisma reto que cujas bases são polígonos regulares.
As arestas laterais de um prisma são segmentos iguais e paralelos entre si. Nos prismas retos são prependiculares às bases.
Classificação dos prismas segundo o polígono das bases
Conforme os polígonos das bases são triângulos, quadriláteros, pentágonos, etc, o prisma chama-se triangular, quadrangular, pentagonal, etc.
Os prismas rectos cujas bases são polígonos regulares chamam-se prismas regulares.
Quer em objetos de uso corrente, quer na Natureza, encontramos com frequência formas prismáticas.

Área do prisma
Área lateral = Perímetro da base x altura
Área total = Área lateral +2 x Área da base
Volume do prisma
O volume de um prisma reto ou oblíquo, é:
Volume do prisma = Área da base x altura
Recordamos que a altura de um prisma é a distância entre as duas bases. Se o prisma é reto, a altura coincide com o comprimento das arestas laterais.
TD
1) Calcule o volume de um cubo que tem 10cm de aresta.
Solução. O cubo possui todas as dimensões com mesma medida. Seu volume é calculado pela fórmula: V = a3 . Logo V = (10)3 = 1000cm3.
2) Um prisma pentagonal regular tem 20cm de altura. A aresta da base mede 4cm. Determine sua área lateral.
Solução. A área lateral é a soma das cinco áreas dos retângulos que são as faces laterais. Como a base é regular, todas as arestas possuem a mesma medida. Logo, temos:
i) Área de uma face: 4 x 20 = 80cm2
ii) Área lateral: 5 x (80cm2) = 400cm2.
3) Um prisma quadrangular regular tem sua aresta da base medindo 6m. Sabendo que a área lateral do prisma mede 216m², calcule sua altura.
Solução. Se o prisma é regular então suas bases são quadradas. A área lateral é a soma das áreas das quatro faces. Temos:
216 = 4x6xh
h =216/24 h = 9
4) Um prisma reto tem por base um triângulo isósceles de 8cm de base por 3cm de altura. Sabendo que a altura do prisma é igual a 1/3 do perímetro da base, calcule sua superfície total.
Solução. No triângulo isósceles a altura também é mediana.
i) Pela relação de Pitágoras temos:

logo a = 5cm
ii) O perímetro da base vale: 5cm + 5cm + 8cm = 18cm
iii) A altura do prisma vale
1/3 x 18 = 6cm
iv) área total
Ab = 8 x 3 /2 = 12cm²
Al = (8x6)+2 x (5x6) = 108cm²
At= 2x 12 + 108= 132cm²
5) Calcule a área total de um prisma reto, de 10 cm de altura, cuja base é um hexágono regular de 6cm de lado.
Solução. A área total de um hexágono regular vale o sêxtuplo da área do triângulo eqüilátero.
Temos: .

Ab =6x (6²x ṛaiz quadrada de3)/4 = 93,5
Al = 6x6x10 = 360
At = 2 x93,5 +360 = 547cm²
6)Um armário, com a forma de um paralelepípedo de dimensões 0,5m, 2,5m e 4m, deve ser pintado. O rendimento da tinta empregada é de 5m² por litro. Determine a quantidade de tinta necessária para pintar toda a parte interna do armário.
Solução. Calculando a área total, temos: .
At = 2x{(0,5)(2,5)+(0,5)(4)+(2,5)(4)} = 26,5m²
Logo, empregando 5m2 por litro, serão gastos 26,5/5= 5,3 litros.
7)A garagem subterrânea de um edifício tem 18 boxes retangulares, cada um com 3,5m de largura e 5m de comprimento. O piso da garagem é de concreto e tem 20cm de espessura. Calcule o volume de concreto utilizado para o piso da garagem.
Solução. O piso terá a forma de um paralelepípedo muito fino, já que sua espessura é de 0,20m. Esse piso entrará em cada box. O volume de cada piso é V = (3,5) x (5) x (0,20) = 3,5m3. O volume total utilizado nos 18 boxes será V = (18) x (3,5) = 63m3.
8) Dispondo-se de uma folha de cartolina, de 70cm de comprimento por 50cm de largura, pode – se construir uma caixa, sem tampa, cortando-se um quadrado de 8cm de lado em cada lado. Determine o volume desta caixa.

Solução. O desenho mostra a parte retirada de cada lado e a caixa construída na forma de um paralelepípedo.
O volume será V = (54) x (34) x (8) = 14688cm3.
Assinar:
Comentários (Atom)